스미스차트 사용법, 임피던스 매칭, how to use smith chart

스미스차트 AI 생성 이미지(Chat gpt)

---

스미스 차트는 임피던스가 어떤 값을 가지고 있는지 보여주는 용도로 주로 사용되지만 과거에는 임피던스 매칭을  하기 위한 중요한 도구로 사용되었다.   이 글에서는 스미스차트의 실제 임피던스 매칭 작업이 어떻게 이루어지는지 글쓴이(DS1ORJ)의 관점에서 기술한다.  보다 자세한 내용은 Chris Bowick 의 RF Circuit Design (Newnes, 1982) 서적 Chapter 4 를 참고한다. 

https://ds1orj.tistory.com/219

아마추어 무선 관련 참고 자료 목록 (RF 설계 관련 서적 및 자료)

 

※ 참고, 스미스 차트는 "계산자(slide rule, 아래 wiki 참고)" 의 원리와 비슷하게 작동한다.

https://en.wikipedia.org/wiki/Slide_rule

Slide rule - Wikipedia

---

 

스미스차트가 인쇄된 종이에 콤파스와 자로 그리면서 매칭 작업을 하는 시대는 지났지만, 아직도 스미스차트로 임피던스를 설명하고 매칭하는 방법이 거의 모든 RF 서적에 전설처럼 등장한다. 

 

이 글에서는 Z = R(저항) + X(리액턴스) 형태의 임피던스 측정 값을 예시로 사용한다.   Z = R + X 형태의 측정 값은 비교적 단순한 구조인 브리지(Bridge, 아마추어 영역에서는 노이즈 브리지, MFJ-259 등의 안테나 분석기 등도 내부적으로 브리지를 사용한다)를 이용하여 측정 할 수 있다

.

※ 브리지의 원리 및 제작 방법은 아래를 참고한다. 

https://ds1orj.tistory.com/153

R - X 노이즈 브리지

 

스미스차트가 무엇인지 전혀 모르겠다면 아래 SimSmith 프로그램을 이용하여 직접 사용해 볼 수 있다. 

https://ds1orj.tistory.com/184

임피던스 매칭 (2) 스미스차트 SimSmith

 

고해상도 스미스차트 이미지는 아래에서 다운 받을 수 있다.  (컬러 버전은 임피던스 + 어드미턴스 차트를 포함한다)

https://leleivre.com/rf_smith.html

PDF Smith Charts

---

가장 먼저 알아야 할 것은 스미스차트로 매칭할 목표 임피던스는 스미스차트의 정 중앙에 1.0 이라는 수치로 표시 된다는 것이다.  따라서 임의 값 부하 임피던스를 50옴 스미스차트 상에 표시 하려면 50 옴이 1.0 으로 표시 되도록 측정 값을 50으로 나눠서 스케일링을 해야하고 이러한 과정을 "정규화" 라고 한다.

 

따라서 50옴으로 매칭하는 경우라면 부하 임피던스를 50 으로 나누면 된다.  이 때 50 은 1.0,  100 은 2.0 이 된다.

100옴으로 매칭할 것이라면 부하 임피던스를 100 으로 나누면 된다.  이 때 100 은 1.0,  200 은 2.0 이 된다.

역으로 스미스차트상에 1.0+0.5 위치에 점이 있다면 정규화된 값을 곱해주면 그대로 임피던스가 된다.

50옴이 정규화 였다면 Z=50+j25 가 될 것이고, 100옴이 정규화였다면 Z=100+j50 이 될 것이다.

 

예를들어 Z = 100+j150 값을 스미스차트에 표시할 경우, 100 옴에 매칭 시키려고 한다면 100 으로 나눠서 정규화를 하게 되고, 좌표값은 1.0+j1.5 가 된다. 만약 동일한 Z = 100+j150 값을 스미스차트에 표시할 때, 50옴에 매칭 시키려고 한다면, 50 으로 나눠서 정규화를 하게 되고, 좌표값은 2.0+j3.0 가 될 것이다. 

 

이러한 Z 값은 복소수로 표현하며 저항(R)은 실수부, 리액턴스(X)는 허수부(j) 값이다. 명시적으로 허수임을 알리기 위해 1.0+j1.5 로 표기하는 것이 관례이다. 수학에서는 허수를 i 단위로 보지만 전자공학에서 i 는 전류이므로  j 를 사용하는 것이 관례이다. 

 

이해를 돕기 위해 부하 임피던스 Z=100+j150 을 위에서 소개한 SimSmith 에서 찍어 보면 아래와 같다. 

기본 정규화 임피던스는 50 옴 이다. (즉, 목표 임피던스, 프로그램 상에서는 G(RF 소스 제네레이터)로 표기됨) 

따라서 부하 임피던스 위치는 2+j3.0 이 된다. (프로그램에서는 정규화 값을 보여주지 않으므로 위치만 확인한다)

 

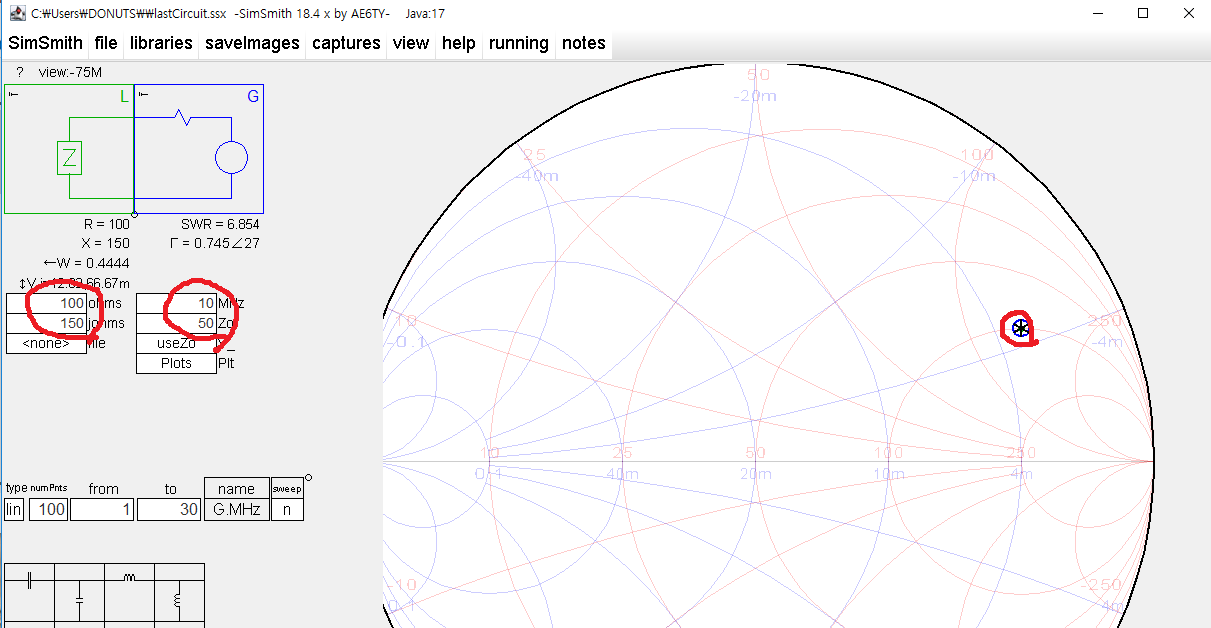
만약 100 옴으로 정규화 하면 아래와 같이 중앙이 50에서 100 옴으로 바뀌고 당연히 부하 임피던스 위치도 변한다.

이제 부하 임피던스 위치는 1+j1.5 가 된다. (프로그램에서는 정규화 값을 보여주지 않으므로 위치 이동만 확인한다)

 

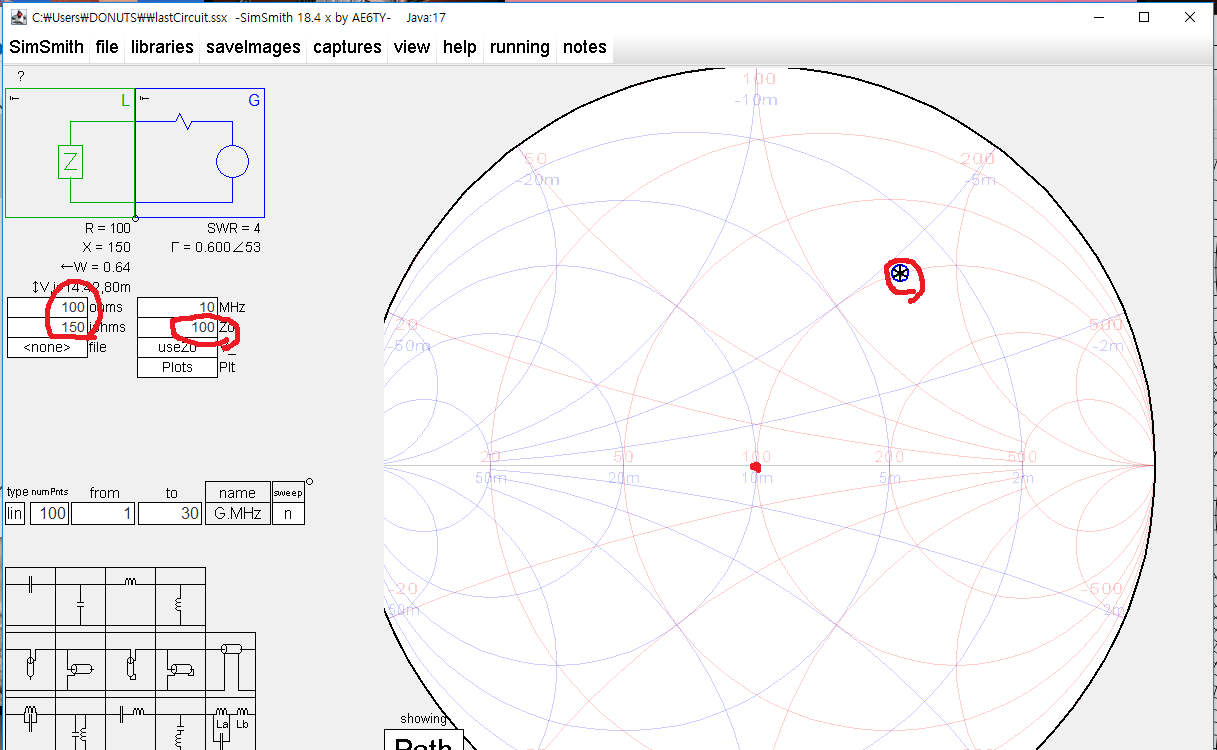
이럴 일은 없겠지만, 부하 임피던스를 100+j150 으로 정규화 한다면 임피던스 매칭이 완료된 것과 다름이 없으므로, 아래와 같이 정중앙 1.0+j1.0 으로 표시 되게 된다. 

---

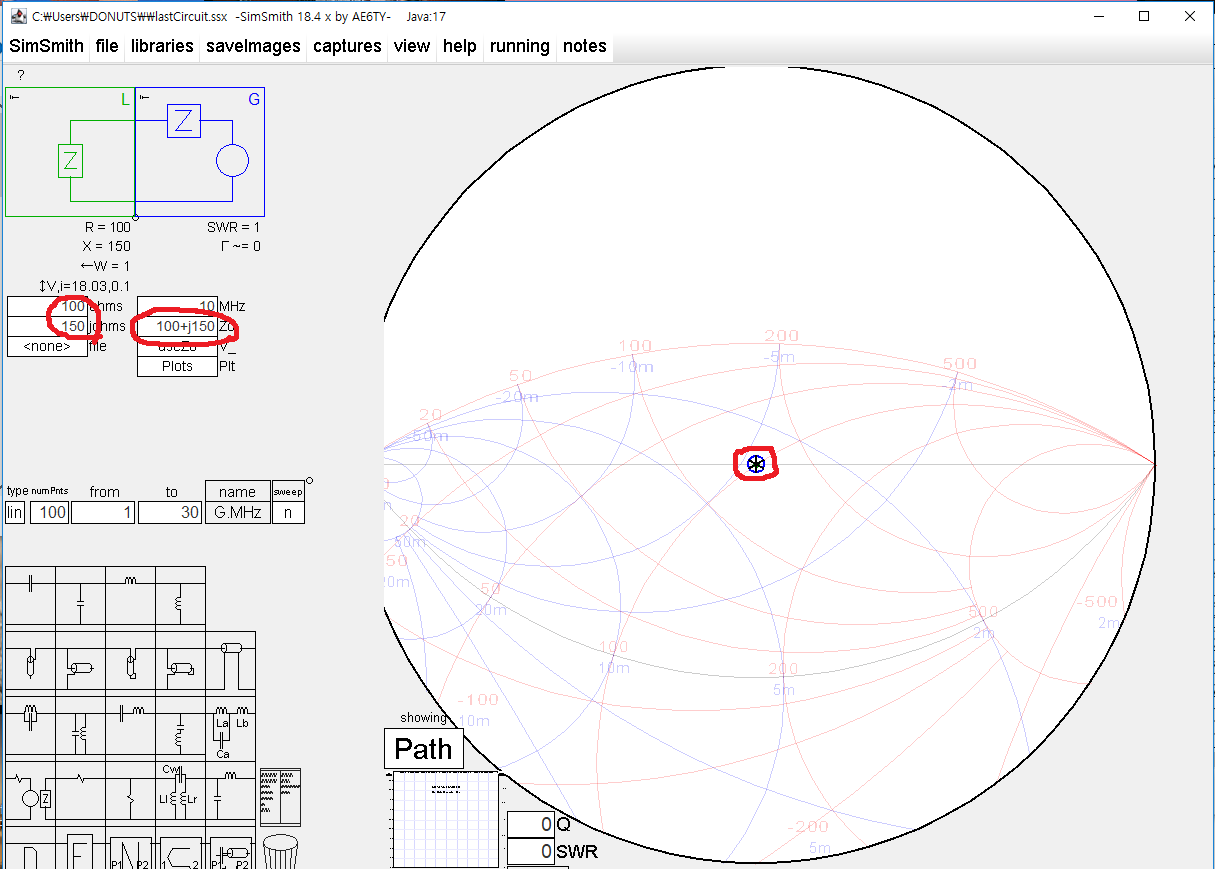
기본 개념을 이해 했다면, 이제 Z=100+j150 을 50 옴으로 정규화하여 스미스차트에  표시해본다.

설명한대로 50 으로 나눠서 구할 수 있으며 결과는 2+j3 이다. 

 

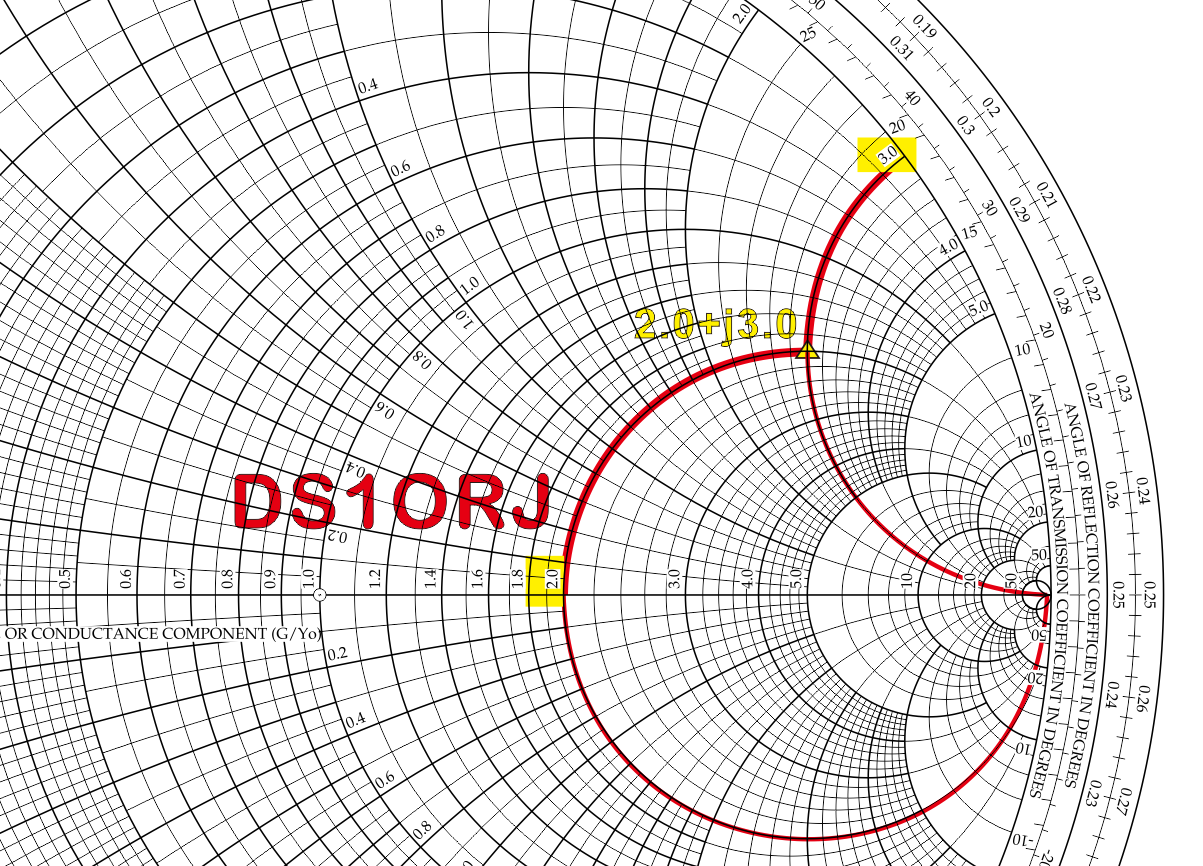
아래와 같이 중앙 원점을 수평으로 가로지르는 선은 "저항" 을 나타낸다. 여기서 2.0 을 선택한다.

오른쪽에서 원 바깥으로 뻗어 나가는 휘어진 선은 리액턴스를 나타낸다. 여기서 3.0 을 선택한다.

(정확한 값은 스미스차트의 테두리 안쪽에 표시되어 있다.) 

두 라인을 쭉 그어서 그려보면 두개의 원이 만나는 지점이 2.0 + j3.0 이며 아래 그림에 표시되었다. 

 

 

일단 부하 위치가 표시되면, 아래와 같이 극좌표 형식인 반사계수 Γ (감마, Gamma, 크기와 각도) 로  쉽게 변환 될 수 있다.

감마에서 크기(Magnitude) 는 아래 그림처럼 중앙의 1.0 원점에서 2+j3 까지 그은 거리가 된다. 이 거리는 스미스차트 하단의 계산자에서 실제 반사계수 크기로 환산 할 수 있다. 스미스차트 인쇄물(종이)의 크기에 따라 이 길이는 변하겠지만, 계산자의 크기도 같이 커지거나 작아지므로 환산 값은 변하지 않는다. 

각도는 스미스차트 바깥쪽까지 직선을 연장하여 원 둘레에 쓰여진 "Angle of reflection coeffcient (반사계수의 각도)" 에서 읽는다. 이 경우 30 과 20 도 사이에 걸쳐 있고 눈금을 자세히 보면 약 27도에 해당하는 것을 알 수 있다.  

 

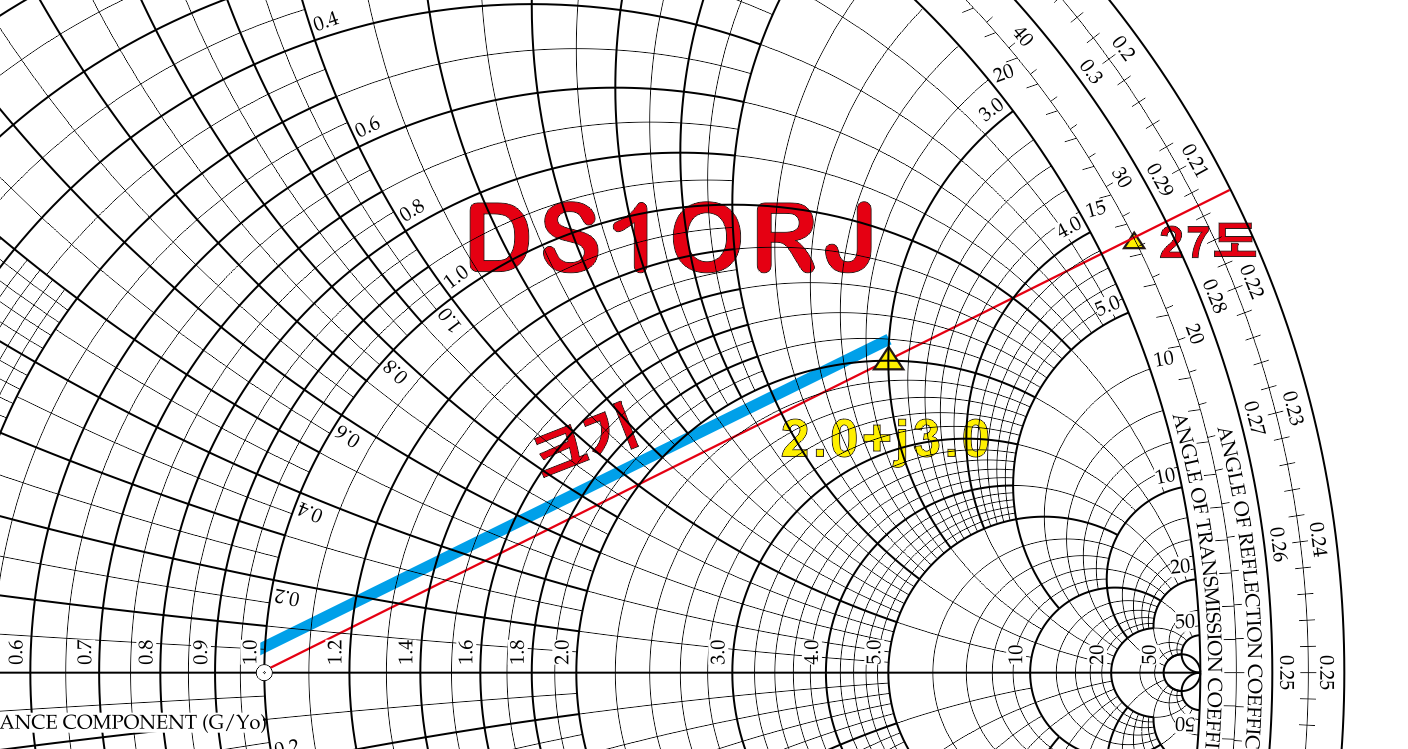
아래와 같이 원래 스미스 차트 하단에는 환산에 필요한 스케일이 준비되어 있다.

콤파스로 원을 그려서 아래로 연결시키면 보다 편하게 값을 변환 할 수 있다.

 

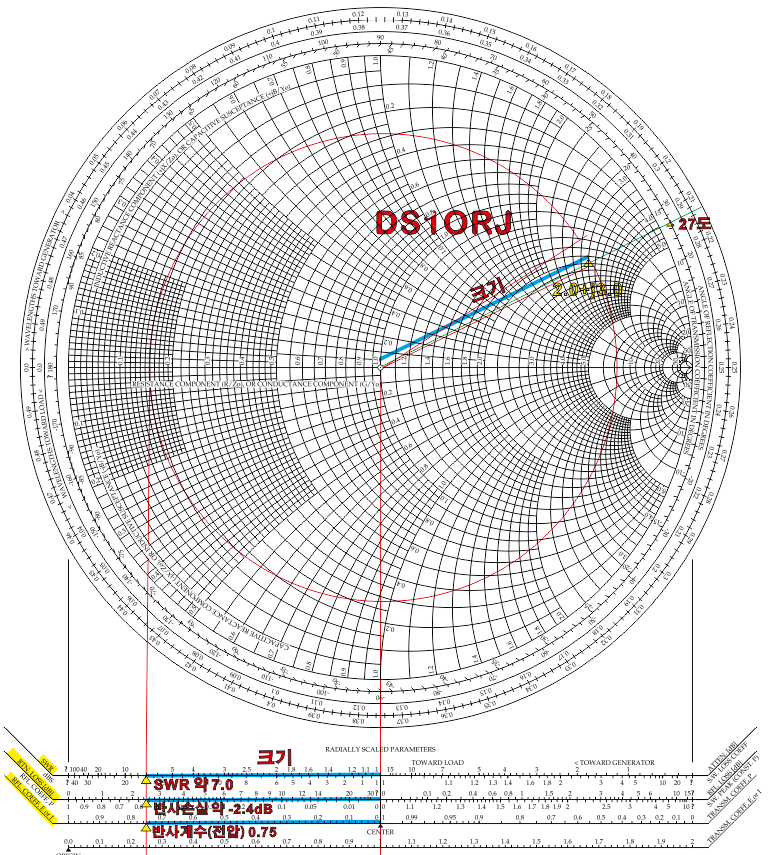
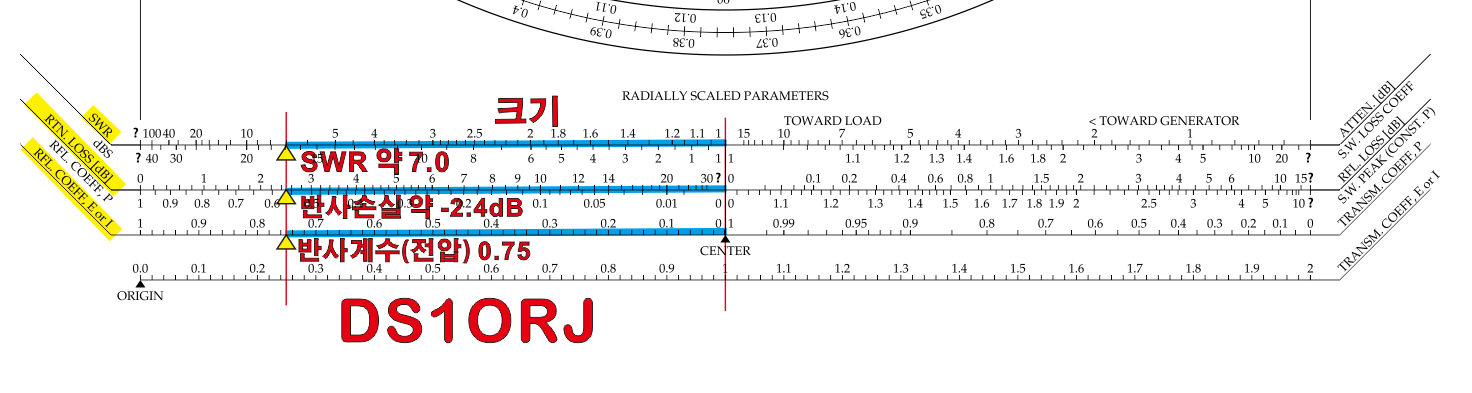
크기를 그대로 대입시켜서 보면 SWR 은 약 7.0 임을 알 수 있고 

그로인한 반사손실은 약 -2.4dB 인 것을 알 수 있다. 

반사계수(Reflection Coefficent) 의 크기(Magnitude)는 약 0.75 이므로, 스미스차트 바깥 원에서 읽은 27도 와 함께 표현 할 수 있다. 이 값은 감마( Γ )라고 부르며  Γ  = 0.75 ∠ 27 이라고 표기한다. 

조금만 더 생각해보면 스미스차트를 이용하여 이 작업을 역으로 진행하여 감마(각도와 크기)를 임피던스로 변환 할 수도 있음을 알 수 있다.

 

 

프로그래밍 가능한 공학용 계산기가 대세인 현재에 이런 작업은 오히려 번거롭기 마련이지만, 계산기가 없는 상황에서 한번에 변환이 가능한 방법은 분명 당시로써는 획기적인 것이다. 

 

Z = 100 + j150 을 계산기로 변환해보면 아래와 같은 결과를 얻는다.(소수점 3자리 반올림)

Γ  = 0.7454 ∠ 26.565

Return loss = -2.553 dB

SWR = 6.854

---

Γ(감마) 와 Z(임피던스) 상호 변환은  아래 계산식을 사용한다.

참고로 안테나와 같은 1포트 네트웍의 S 파라미터를 측정할 경우, 측정된 S11 값은 반사계수 감마 값과 일치한다.

따라서, 이 경우 S11 값을 감마로 간주하고 아래 수식을 통해 임피던스로 변환 할 수 있다.  

※ 아래 수식에서는 50옴 정규화를 사용한다. 만약 다른 값의 정규화를 사용했다면 50을 해당 값으로 변경한다.

Γ 와 Z 모두 복소수로 취급되므로 계산기에 입력시 복소수 입력방법을 따라야 한다.

 

Γ 를 Z 로 변환 : Z = 50 * ((1 + Γ) / (1 - Γ))  

Z 를 Γ 로 변환 : Γ = (Z - 50) / (Z + 50)

반사손실 dB :  dB = 20 * Log10(|Γ|) 

SWR 로 변환 : SWR = (1+|Γ|) / (1-|Γ|) 

---

 

스미스차트를 이용한 임피던스 매칭 

 

임피던스 매칭은 다양한 방법(스미스 차트상의 다양한 경로와 모양)이 있지만 아래서는 가장 간단한 경로를 선택한 그림이다. 오른쪽 중심을 향하는 임피던스 서클과 대칭되는 왼쪽 파란색 서클들이 보이는데 이 원들은 어드미턴스를 나타낸다.  (스미스차트는 임피던스만 표시된 경우도 있고 어드미턴스와 함께 표시된 것도 있다.)

여기서 어드미턴스(Y)는 임피던스(Z) 의 역수이므로 임피던스가 무한대가 되면 어드미턴스는 0 이다. 임피던스가 0 이면 어드미턴스는 무한대이다. 어드미턴스에도 임피던스처럼 리액턴스(X)를 나타내는 값이 있으며, 서셉턴스(B) 라고 부른다.

 

 

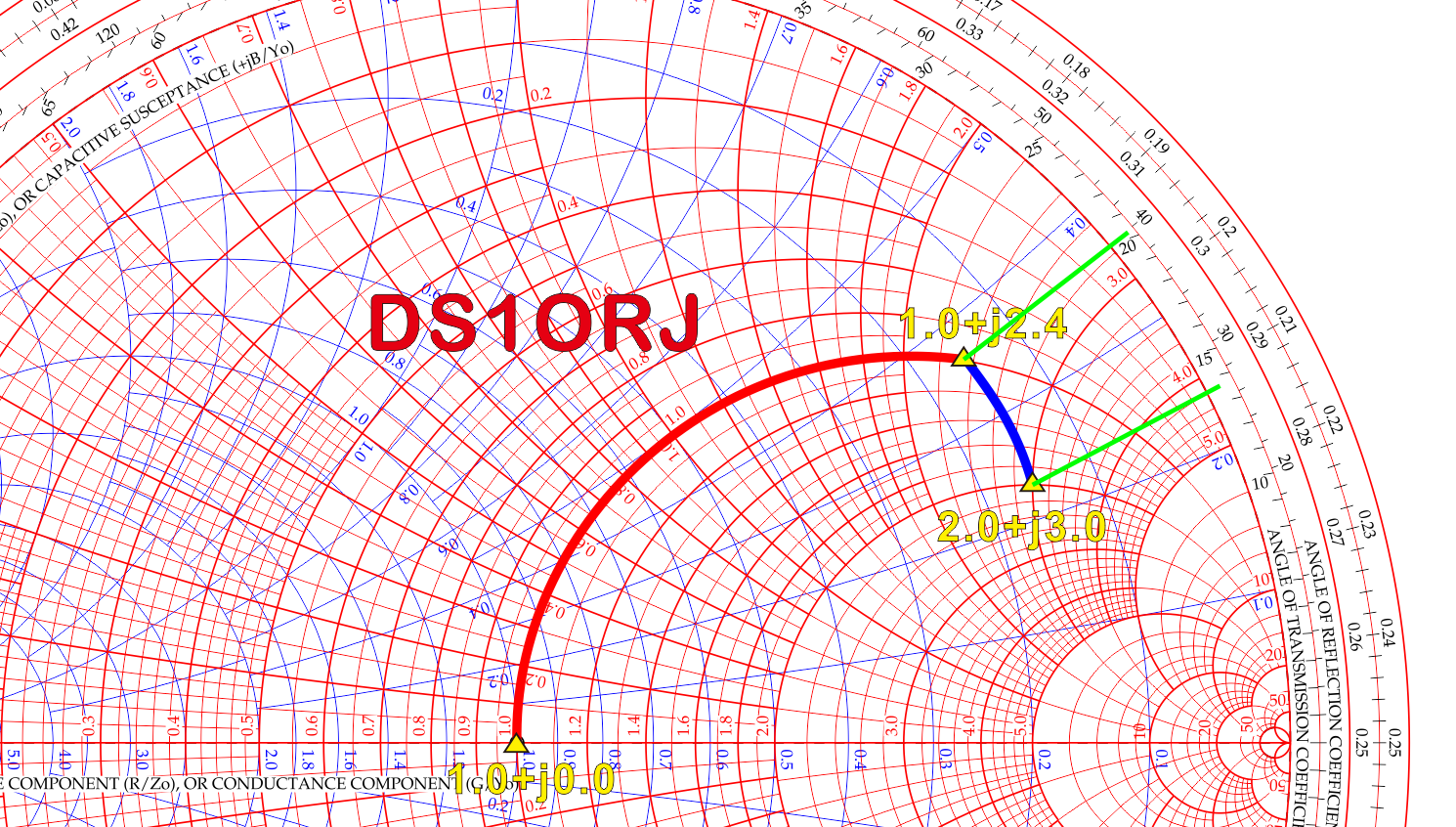
임피던스 매칭은 부하임피던스를 스미스 차트의 중심으로 옮겨오는 작업이다.

글쓴이가 선택한 경로는 다음과 같다. 부하인 2.0+j3.0 에서 파란색 서셉턴스 경로를 타고 1.0+j2.4 로 이동한다. 어드미턴스 차트의 서셉턴스 경로는 병렬로 L 또는 C 를 연결하면 이동하게 되는 경로이다.  여기서는 반시계 방향(위)으로 움직였으므로 병렬 L 에 해당한다. (아래 시계방향으로 가면 병렬 C 이다) 

1.0+j2.4 에서 1.0+j0.0 의 중심까지 붉은색 경로는 임피던스 차트의  리액턴스 경로이다. 이 경로는 직렬로 L 또는 C 를 연결하면 이동하게 되는 경로이며 여기서는 반시계 방향(아래)으로 움직였으므로 직렬 C 에 해당한다. 회전 방향이 반대가 되면 직렬 L 이 된다. (어드미턴스와 반대인 것을 알 수 있다)

최종적인 임피던스 매칭 회로의 형상은 부하와 병렬로 L, 직렬로 C 가 연결된 모양이 된다.  

 

※ L 이나 C 가 부하와 연결되는 방식에 따른 회전 방향은 아래를 참고한다. (RF Circuit Design) 

 

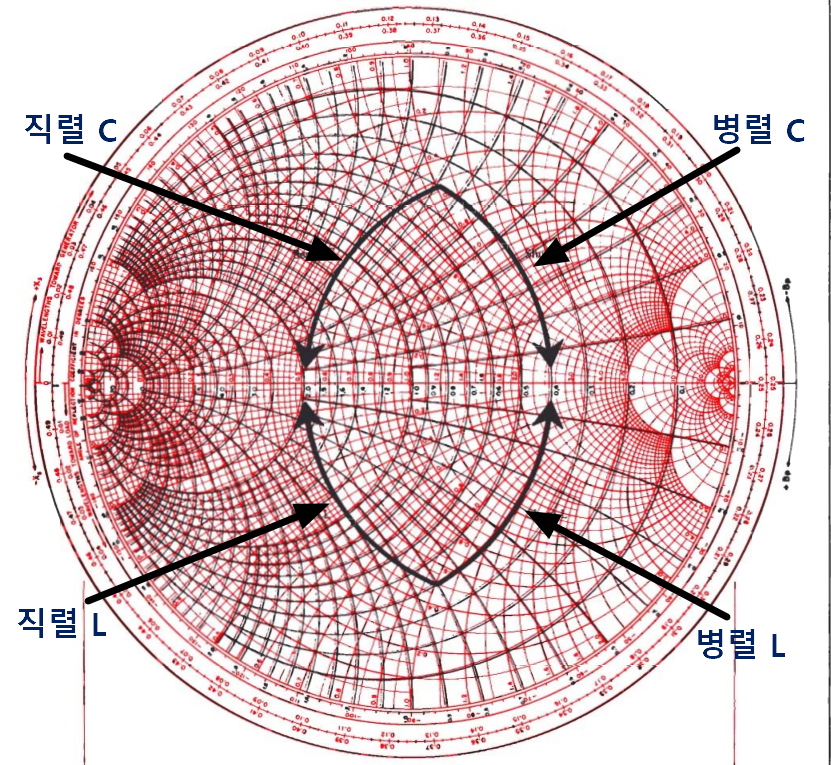
리액턴스 서클(직렬연결)에서는 시계방향이면 직렬 L 이고, 반시계면 직렬 C 이다. 

서셉턴스 서클(병렬연결)에서는 시계방향이면 병렬 C 이고, 반시계면 병렬 L 이다. 

원을 타고 도는 것을 잘 보면  L 은 항상 스미스차트 위로 올라가는 방향이고,  C 는 항상 아래로 내려가는 방향이 된다.

(RF Circuit Design Fig 4-39, p.89) 

---

 

이제 스미스 차트에서 읽은 값을 실제 값으로 환산하는 단계이다. 

 

파란색 경로(병렬 L) 값은 서셉턴스 원에서 0.24 에서 0.37 까지 걸쳐 있는 것을 알 수 있다. 

이 길이(서셉턴스 값)를 구해보면, 서셉턴스 B 값은 0.37-0.24 = 0.13 이 된다..  

빨간색 경로(직렬 C) 값은 리액턴스 원에서 2.3 에서 0 까지 연결되어 있다. 따라서 리액턴스 X 값은 2.3-0 = 2.3 이다. 

 

스미스차트에 표시된 리액턴스 또는 서셉턴스 값으로부터 L, C 값을 계산하려면 아래 공식을 사용한다. 

스미스차트 값들은 "정규화" 되어 있으므로 계산에는 정규화에서 사용했던 값을 곱하는 것이 기본이다. 

※ F 는 주파수이다. N 은 정규화에 사용했던 값(일반적으로 50) 이다.

직렬 연결된 리액턴스(X) 값으로 구하는  C 값은 1 / (2*pi*F*X*N), L 값은 (X*N) / (2*pi*F) 이다. 

병렬 연결된 서셉턴스(B) 값으로 구하는  C 값은 B / (2*pi*F*N), L 값은 N / (2*pi*F*B) 이다.

 

상기 스미스차트에서 읽은 대로 병렬 L 의 서셉턴스 B=0.13, 직렬 C 의 리액턴스 X=2.3 이다. 

10MHz 에서 Z = 100+j150 을 50옴으로 매칭하는데 필요한 값을 수식에 대입하여 구하면 아래와 같다.

※ 리액턴스나 서셉턴스를 L, C 값으로 변환하려면 주파수가 반드시 지정되어야 한다. 

병렬 L 값 uH  = 50 / (2*pi*10*0.13) = 6.12 uH.

직렬 C 값 uF = 1 / (2*pi*10*2.3*50) = 0.000138 uF = 0.138nF = 138pF.

 

해당 값을 SimSmith 에 입력해서 그려보면 아래와 같이 거의 50옴에 가깝게 매칭된 것을 알 수 있다.

※ 차후 다른 글에서 설명하겠지만,  단순 LC 매칭은 스미스차트의 도움 없이 계산기만 가지고 수행 할 수 있다.

 

 

---

 

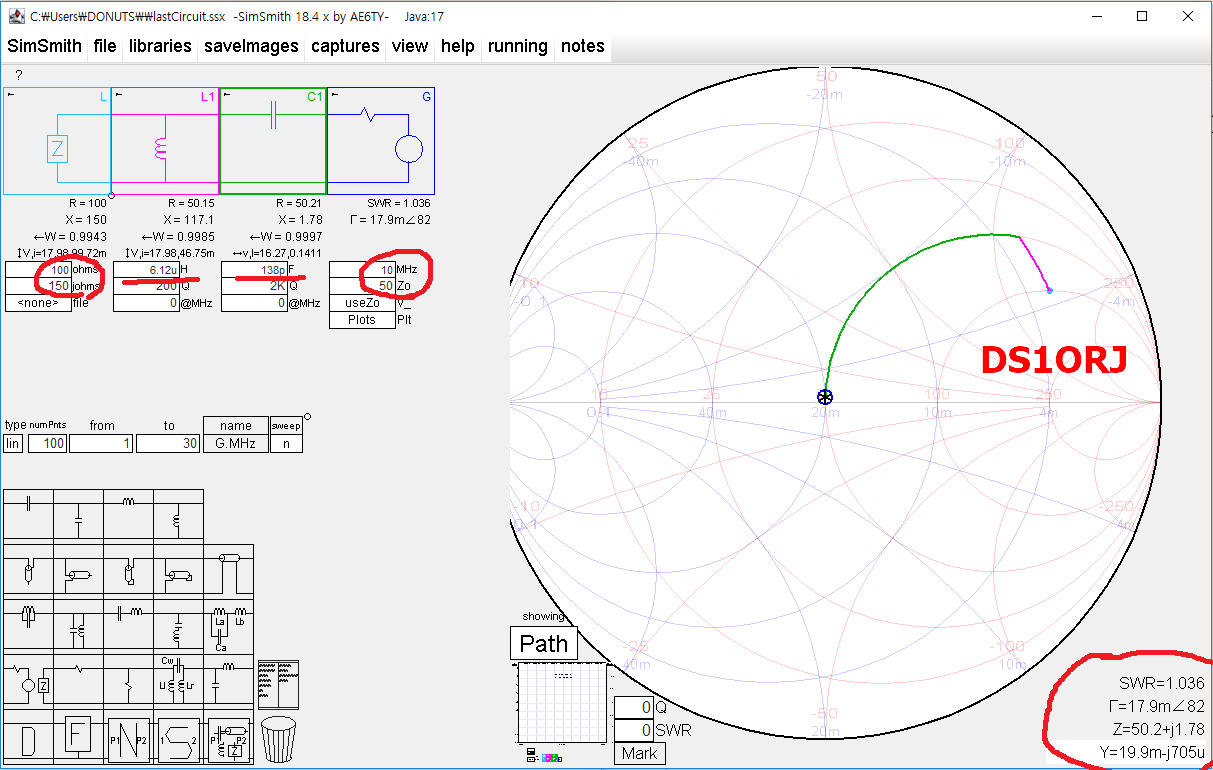
살펴본 바와 같이 우리는 임피던스 매칭 경로를 선택할 때 서셉턴스(어드미턴스, 병렬연결) 서클을 타고 돌 것인가 또는 리액턴스(임피던스, 직렬연결) 서클을 타고 돌 것인가 결정 해야만 하고, 그 다음은 어느 방향(L 또는 C)으로 회전할지 결정해야 한다.

이 결정은 L  을 먼저 사용할 것인가 C 가 먼저인가와 연관되어 있으며(둘 중 어느것을 먼저 하더라도 매칭은 된다)  이 결정에 따라  매칭 네트웍이 Low Pass 또는 High Pass 작용을 하게 된다.(특별한 경우가 아닌 이상 대부분 고조파 하모닉을 줄일 수 있는 Low Pass 를 선택하게 된다.) 

 

※ 단순한 L 네트웍 매칭은 아래서 설명하는 RFSim99 로 자동으로 계산하고 시뮬레이션 할 수 있다. 

https://ds1orj.tistory.com/162

임피던스 매칭 (1) RFSIM99 사용

 

 

※ 이 글과 이어지는 아래 글에서는 수식과 계산기를 사용하여 L 또는 T 네트웍으로 임피던스를 매칭하는 방법에 대해 기술한다.

https://ds1orj.tistory.com/232

임피던스 매칭 공식, Impedance Matching Formula, 공학용 계산기, CASIO 9860, 9750