보통 임피던스는 Z = R + X 또는 Z = R + j 형태로 표기된다.
우리는 임피던스 Z 가 "교류저항" 임을 이미 알고 있다.
즉, Z 가 1 옴 이라면, 일반적인 저항 1 옴과 같은 것처럼 보인다.
아래처럼, 캐패시터가 됐든 1옴 저항이 됐든 임피던스 1 옴은 1V 에서 1A 전류가 흐른다.

따라서 둘 다 임피던스 Z 는 1 옴 이다.
재밌는 것은, 상기 회로에서 두 부품의 임피던스가 모두 1 옴 이므로 두개를 직렬 배치하면 2 옴이 될거 같지만 실제로는 그렇게 되지 않는다.
아래서 보는 바와 두 부품을 직렬 연결하면 1A 의 절반인 0.5A 만 흘러야 하지만 0.7A 넘는 전류가 흐르는 것을 볼 수 있다. (약 0.707A)

이러한 현상이 발생하는 이유는 C1 이 실제 저항으로 작동하는 것이 아니고 "저항인 것처럼" 행동하기 때문이다.
저항과 캐패시터가 직렬 연결되면 캐패시터의 충방전 회로에 저항이 추가되므로 단순히 직렬 저항이 되는 개념으로는 정확히 계산 할 수 없다는 것을 알 수 있다.
이런 계산상 문제 때문에 Z = R + X 라는 복소수(complex) 형태로 표기하고, 복소수 형태로 더하거나 빼게 된다.
왜 그런지 이해가 되지 않을 것이므로 아래를 본다.
1 옴 저항만 있는 경우 1W 를 소모한다.(물론 교류이므로 0~1V 사이에 변동한다, 붉은색)

그러나 아래처럼 캐패시터만 있는 경우는 전원 극성에 따라 +0.5W 와 -0.5W 를 왔다갔다 한다.
쉽게 말해 "충방전"을 반복한다. 소모전력을 합치면 0W 이다(소모전력은 없다.)
즉, 전류는 흐르지만 소모는 하지 않는다. (전력을 일시적으로 보관 했다가 전원으로 되돌린다. 100% 반사, 역률 0)

우리가 일반적으로 계산하는 옴의 법칙은 "실수" 를 기준으로 사용하므로 복소수 Z (R+X 형태) 를 그대로 가져다 쓰면 결과가 복잡해진다.(일반 계산기로 되지 않는다), 편의상 보통 "임피던스 값" 이라고 하는 것은 복소수 임피던스 Z 가 아닌 임피던스 Z 의 크기를 주로 사용하고 단순히 "몇 Ohm" 이다 라고 표기한다. (이렇게 함으로써 계산을 단순화 할 수 있다.)
즉, 단순 표기된 "임피던스 몇 옴" 이라는 것은 "임피던스의 크기" 를 의미한다고 생각하면 된다.
Z 의 크기는 아래와 같이 쉽게 계산 할 수 있다.
Z=√R2+X2
이 글의 처음에서 본 회로, 저항이 1 옴이면 임피던스(크기)는 1 옴이다.
Z=√R2+X2=√12+02=1
그리고 캐패시터의 리액턴스가 1 옴이면 여전히 임피던스(크기)는 1 옴이다.
Z=√R2+X2=√02+12=1
즉, Z = R + X 에서 R 또는 X 가 0 이면 계산할 필요도 없이 Z 크기는 R 또는 X 가 된다.
그러나, 아래와 같이 1옴 저항과 1옴 캐패시터가 합성(직렬)이 되면 2 옴이 아니고 약 1.414 가 된다.
Z=√R2+X2=√12+12=1.414..
따라서, 1옴 저항과 1옴 캐패시터가 직렬된 경우 전류는 0.5A 가 아니고
I=E/R=E/Z=1/√2=1/1.414..=0.7071.. 약 0.7071.. A 가 된다.
다소 복잡해 보이지만 "임피던스의 크기" 를 구하면 옴의 법칙이 성립 한다는 것을 알 수 있다.
여기서 왜 직렬 연결을 복잡하게 "제곱" 을 동원해서 계산해야 하는가 의문이 들 수 있다.
아래처럼 그냥 더하기로 편하게 계산 할 수 없을까?

실제 리액턴스 X (캐패시터 또는 코일)는 충방전을 하고 R 은 X 의 충방전을 방해하므로 아래처럼 일정 영역이 겹치게 된다. 그래서 단순 더하기로는 정확한 값을 얻을 수 없다.

좀 더 정확히 표현하자면 아래와 같이 된다.

위의 그림은 흔히 말하는 "벡터(Vector)" 표현 이다.
만약 R 또는 X 가 0 이 되면 각각 아래와 같다.

저항 R 이 없고 리액턴스 X 만 있을 경우 각도는 90 도 이고 Z 크기는 X 와 같다.
또는 아래와 같이 저항만 있는 경우 각도는 0 이고 Z 크기는 R 과 같다.

위의 경우를 제외하고 R + X 가 모두 포함될 경우에는 두 값의 사이를 "가로지르는 거리" 즉 벡터를 알아야 하므로 복잡해지는데 이것이 앞서 설명한 임피던스의 크기 이다.
이 거리를 편하게 계산하는데 "피타고라스의 정리" 공식을 사용할 수 있고. 그것이 바로 전술한 Z 크기(거리) 를 계산하는 Z=√R2+X2 공식이다.
또한 여기서 얻어진 Z 크기는 복소수가 아니므로 그대로 일반 계산에 사용 가능하다.
상기 계산에서 "각도" 라는 표현이 나오는데 전압은 항상 같은 각도로 공급되므로 이 "각도" 라는 것은 회로에 흐르는 전류의 각도이다. 즉 전압과 전류의 위상차를 얘기한다.

다시 한번 위의 벡터를 보면 알 수 있는 사실은 아래와 같다.
- R 과 X 값을 알면 각도와 Z 크기를 계산 할 수 있다.
Z = R + X 만 알고 있을 때 삼각함수를 이용하여 위상을 계산하려면 아래와 같다.
XR=tan θ 이므로 θ=tan−1(XR)
XZ=sin θ 이므로 θ=sin−1(XZ)
RZ=cos θ 이므로 θ=cos−1(RZ)
- Z 크기와 각도를 알면 R 과 X 를 역으로 계산 할 수 있다.
Z=√R2+X2=Xsin θ=Rcos θ
X=√Z2−R2=Z∗sin θ=R∗tan θ
R=√Z2−X2=Z∗cos θ=Xtan θ
상기 수식에서 RZ 은 흔히 말하는 "역률(Power Factor) " 이다.
즉, 전체 임피던스에서 실제 저항(리액턴스를 제외한)이 소모한 전력을 의미한다.
1 이면 공급된 전력은 모두 소모 되었고 Z = R 이고 X 는 0 인 상황이다.
이 때 전압과 전류는 동위상 이다. (즉, 차이가 나지 않는다. 0도)
0 이면 공급된 전력은 모두 반사 되었으며(소모전력이 없음) Z = X 이고 R 이 0 인 상황이다.
이 때 전압과 전류의 위상차는 90도 이다.

상기 회로에서 역률은 Z 크기로부터 다음과 같이 계산 할 수 있다.
1√12+12=0.707...
또한 RZ=cos θ 이므로 위상차는 θ=cos−1(RZ) 이다.
위상차를 계산해보면 cos−1(1√12+12)=45 를 얻는다.
일반적인 역율로 표현 할 때 cos 45 가 되고 이는 약 0.707 에 해당한다.
아래는 해당 회로에서 전압과 전류의 위상차가 발생하는 모습
이것은 캐패시터이므로 전류 위상이 앞서간다.(즉, 진상 역률)
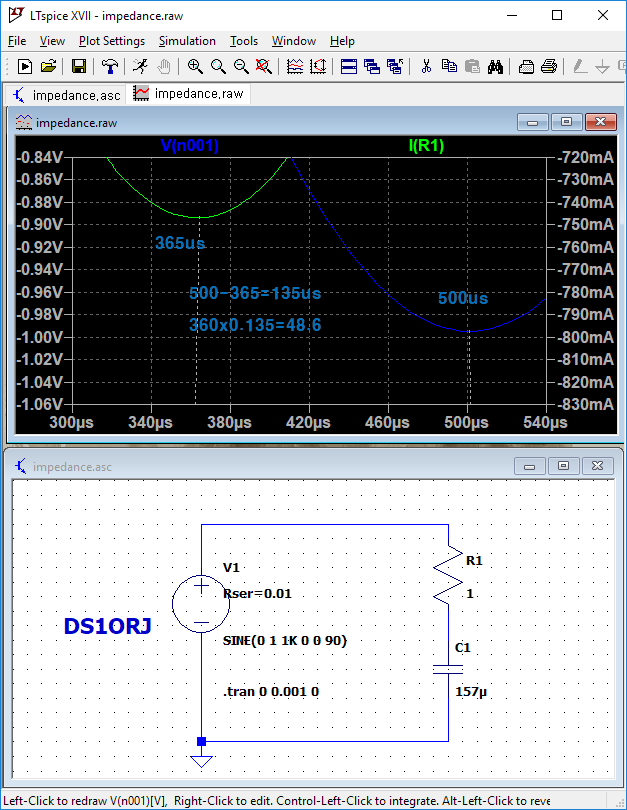
약 48.6 도 앞서 가는데 이것은 시뮬레이션 그래픽 출력에서 수동으로 위치값을 찍은 것이므로 오차가 있다.
※ 이 글에서는 편의상 설명하지 않았지만 리액턴스에는 캐패시턴스(캐패시터, 콘덴서) 와 인덕턴스(인덕터, 코일) 의 두 종류가 있으며 각각 반대 방향으로 움직인다.
즉, X 가 캐패시턴스의 경우에는 음의 값 즉 -X 가 되고, 인덕턴스의 경우에는 +X 즉 양의 값을 가진다.
일반적인 상황, 즉 옴의 법칙 등을 계산하기 위해 "임피던스의 크기" 만 취할 때에는 이 부호의 의미는 없다.
RF 회로에서 임피던스 매칭과 같이 복소 임피던스를 계산할 경우에는 실수부와 허수부가 별도로 계산되고 합쳐지므로 이 때에는 부호가 중요해진다. 예를들면 X 가 10 이라고 할 때 -X(10) 은 +X(10) 과 더해지면 0 으로 사라진다.
전기 분야와 RF 분야가 Z 와 Z 크기를 혼용해서 사용하지만, 전기 분야는 주로 옴의 법칙을 이용해서 기술하므로 Z 의 크기(원칙상 |Z| 로 표시) 를 주로 사용하고, RF 분야에서는 위상 정보도 필요하므로 복소 형태(R+X) 를 주로 사용한다.

