이 글에서는 4NEC2 를 이용하여 베이스 로딩 수직 안테나를 만드는 과정에 대해 기술한다.
시뮬레이션에 사용되는 안테나는 "완전도체" 평면에서 작동하는 것으로 가정되므로 실제와는 다르다.
실제로는 완전도체 대신 레디얼이 사용되며 상황에 따라 다를 것이므로 임피던스 매칭에 실측정치(VNA)를 사용해야 한다.
※ 단축이 많이 된 경우(특히 HF 로우밴드) 임피던스가 극단적으로 낮으므로 아마추어 무선 용도로 사용되는 측정기로는 정확한 값을 알기는 어려울 것이다.
이 글에서 기술하는 것은 4NEC 로 단축 수직 안테나(베이스로딩)를 만들고 임피던스 매칭을 하는 과정이다.
수직 단축 안테나의 작동에 대해 이해하고 개선점을 찾는데 도움이 될 수 있다.
아래 순서대로 설명한다.
1. 코일 및 캐패시터 Q 에 대한 개념 및 영향
2. 단축된 안테나의 임피던스 및 매칭
3. 단축된 안테나의 방사효율과 로딩코일의 Q
1. 코일 및 캐패시터 Q 에 대한 개념 및 영향
흔히 Q 는 품질계수 라고 한다. 이 값은 손실과 관련 있으며 "얼마나 좋은가?" 의 척도로 사용된다
임피던스 Z=R+X 에서 100% 순수한 코일과 캐패시터라면 R 은 0 이고 Z=0+X 로 표시될 수 있다.
여기서 X 는 해당 주파수에서의 리액턴스(옴) 이다.
그러나 실제로는 코일에 저항이 존재하고 캐패시터도 내부적으로 저항(ESR:등가직렬저항)이 존재하므로 결국 R+X 가 된다. X 는 리액턴스 이므로 손실이 없고, 저항 성분인 R 은 전력을 소모하므로 손실을 일으킨다.
X 를 R 로 나누면 손실 비율을 알 수 있고 이것이 바로 Q 값이다. 즉, Q = X / R 이다.
품질계수 Q=XR
L 이나 C 의 리액턴스 X (단위 옴)는 주파수에 의존하는 값이므로 단순히 L, C 값 만으로 이것을 알 수 없으며 반드시 주파수가 주어져야 한다. 그래서 아래와 같이 계산 할 수 있다.
코일(인덕터)의 Q=2×π×f×LR
캐패시터의 Q=12×π×f×C×R
위 관계식에서 보면 코일(인덕터)의 경우에는 주파수가 증가하면 리액턴스가 증가므로 R 값이 고정이면(예컨대 1옴) Q 가 증가할 것이라고 추정 할 수 있다. 캐패시터는 역수이므로 그 반대인데 R 값이 고정인 경우(예컨대 1옴) 주파수가 증가하면 Q 값이 감소한다.
실제로는 L (인덕터) 의 경우 권선이 감긴 형태이므로 주파수가 높아지면 표피효과(skin effect) 로 인해 손실이 점점 더 증가하므로 R 이 고정이 되지 않는다. 캐패시터 역시 유전체 손실로 인해 R 이 증가한다.
따라서 모든 주파수에서 균일한 Q 값은 존재하기 어려우며 주파수에 따라 달라진다.
일반적으로 제시되는 부품의 Q 값은 지정된 주파수(예를 들면 1MHz)에서 측정되며 해당 주파수에서만 유효한 값이다.
코일의 경우 DC 저항을 정밀하게 측정함으로써 직렬저항(R) 성분을 어림짐작 해볼 수 있다.(상기 설명대로 표피효과로 인해 이 값보다 훨씬 더 커진다.)
2. 단축된 안테나의 임피던스 및 매칭
아래는 완전도체 상의 2미터 길이 7메가 수직 안테나의 시뮬레이션이다.
엘레먼트 재질은 알루미늄(전도도 3.7665E7) 1mm 를 사용한다. (다른 두께의 결과는 아래에 첨부된다)

임피던스가 1.23 -j1562 이므로 매우 낮은 방사 저항을 갖는다.
이득은 약 3.95 dBi 이다.
참고로 1/4 파장(10미터 길이)로 지정하면 아래와 같이 약 4.94 dBi 이다, 약 5 dBi.

2 미터로 줄인 안테나는 3.95 dB 이므로 정상적인 10 미터 안테나와 -1 dB 밖에 차이가 나지 않는데 이 값은 매우 좋은 것이다. 이런 결과가 나온 이유는 아직 임피던스 매칭 회로가 적용되지 않았으므로 손실이 반영되지 않았기 때문이다. 다시 말해서 급전 계통에 무손실 환경이 제공된다면 10 미터와 2 미터 안테나는 1 dB 정도 밖에 차이가 나지 않는다. (완접도체 접지 상황에서 시뮬레이션 수치) 실제로는 임피던스 매칭 없이는 급전이 불가능하므로, 아래와 같이 매칭을 한다.
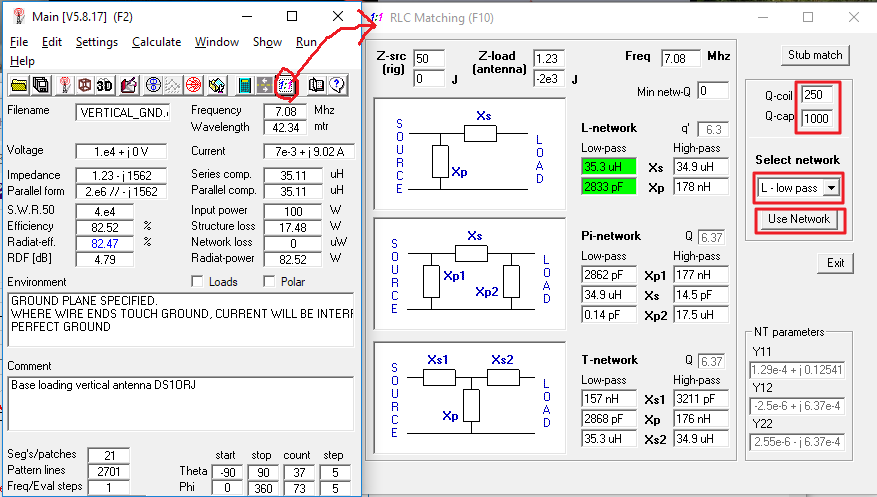
1:1 을 누르고 Q 값을 지정하고 사용할 매칭네트웍(여기서는 L 매칭 로우패스)을 선택하고 "Use Network" 을 누르면 실행 창이 뜨고 Generate 를 누르면 갱신된 결과를 볼 수 있다.
기본 Q 값인 코일 250, 캐패시터 1000 에서 아래와 같은 결과를 얻는다.
이득은 -3.9 dBi 임피던스는 8.38 -j 7.69 이다.

이득이 -8 dB 가까이 떨어진 이유는 Q 값이 너무 낮기 때문인데, 둘 중에 특히 코일의 Q 값 250 이 문제가 된다.
7.08 MHz 에서 35.3 uH 는 리액턴스가 약 +1570 옴이고 1570 / 250(Q값) = 6.28 즉, 코일 저항이 6.28 옴 임을 나타낸다.
또한 이 손실로 인해 50옴 까지 매칭을 하지도 못한다. 방사효율은 13.46% 에 불과하다.
3. 단축된 안테나의 방사효율와 로딩코일의 Q
따라서 코일의 저항이 방사효율을 높이고 정확한 매칭을 제공하는데 매우 중요하다는 것을 알 수 있는데 코일의 손실(Q 수치) 과 방사효율의 관계는 아래와 같다.
수직 엘레먼트 2 미터 두께 1mm
필요한 로딩코일 35.3uH (+1570옴)
| 코일의 Q 값 | 임피던스 | 이득 | 방사효율 |
| 1570/4옴 = Q 는 392 | 12-j7.47 | -2.4 dBi | 19.31% |
| 1570/2옴= Q 는 785 | 19.4-j6.66 | -0.3 dBi | 31.29% |
| 1570/1옴= Q 는 1570 | 27.9-j5.33 | +1.35 dBi | 45.29% |
| 1570/0.5옴 = Q는 3140 | 35.8-j3.67 | +2.45 dBi | 58.34% |
| 1570/0(무손실) = Q는 무한대 | 49.7-j0.06 | +3.92 dBi | 81.96% |
상기 도표를 보면 로딩 코일이 무손실이 아니라면 사실상 50 옴으로 매칭이 불가능한 것을 알 수 있는데, 실제로는 차량용 단축 안테나에서도 50옴에 가깝게 떨어지는 것을 볼 수 있다. 이런 경우 50 옴을 구성하는 대부분의 저항 성분은 레디얼이나 차체 저항에서 온다. (또 다른 손실의 원인)
35uH 를 만들기 위해서는 50mm 직경을 사용할 경우 26 턴, 길이는 4.2 미터를 감아야 하는 것으로 계산된다. (아래 에어 인덕터 계산기 참고), 이 값으로 7MHz 에서의 표피효과를 고려한 와이어 두께별 추정치는 아래와 같다.
1mm 와이어 : 7MHz 에서 0.933 옴, Q 1682.
1.5mm : 0.617 옴, Q 2544
2mm : 0.46 옴, Q 3413
2.5mm : 0.3677 옴, Q 4269
https://ds1orj.tistory.com/185
공심 코일 에어 인덕터 계산기
필요한 인덕턴스 (L) : nH uH 코어 직경 (D) : inch mils mm 와이어 두께(권선직경) (d) : inches mils mm 감긴 폭 (W): inches mils mm 회전 수 (N): 필요한 와이어 길이: 미터(M) 여러번 사용 후 90~95% 이상..
ds1orj.tistory.com
아래부터는 수직 엘레먼트 두께에 따른 이득 변화이다.
수직 엘레먼트 2 미터 두께 10mm
필요한 로딩코일 24.2 uH (+1076옴)
| 코일의 Q 값 | 임피던스 | 이득 dBi | 방사효율 % |
| 1076/4옴 = Q 는 269 | 10.4 -j6.9 | -2.2 | 19.95 |
| 1076/2옴= Q 는 538 | 17.2 - j6.35 | 0 | 33.11 |
| 1076/1옴= Q 는 1076 | 25.6-j5.33 | +1.72 | 49.41 |
| 1076/0.5옴 = Q는 2152 | 33.8-j3.95 | +2.95 | 65.54 |
| 1076/0(무손실) = Q는 무한대 | 49.7-j0.19 | +4.67 | 97.28 |
수직 엘레먼트 2미터 두께 100mm
필요한 로딩코일 12.8 uH (약 +570 옴)
| 코일의 Q 값 | 임피던스 | 이득 dBi | 방사효율 % |
| 570/4옴 = Q 는 142.5 | 9.7 -j6.64 | -2.4 | 18.99 |
| 570/2옴= Q 는 285 | 16.3-j6.23 | -0.2 | 31.95 |
| 570/1옴= Q 는 570 | 24.6-j5.41 | +1.63 | 48.32 |
| 570/0.5옴 = Q는 1140 | 33-j4.23 | +2.91 | 64.95 |
| 570/0(무손실) = Q는 무한대 | 49.6+j0.04 | +4.75 | 99.05 |
참고로 Q 에 따른 SWR 1.5 대역폭(중심주파수 7.08)은 추정치 아래와 같다.(아래와 같이 매칭 회로만 SimSmith 에서 별도로 시뮬레이션한 결과치)
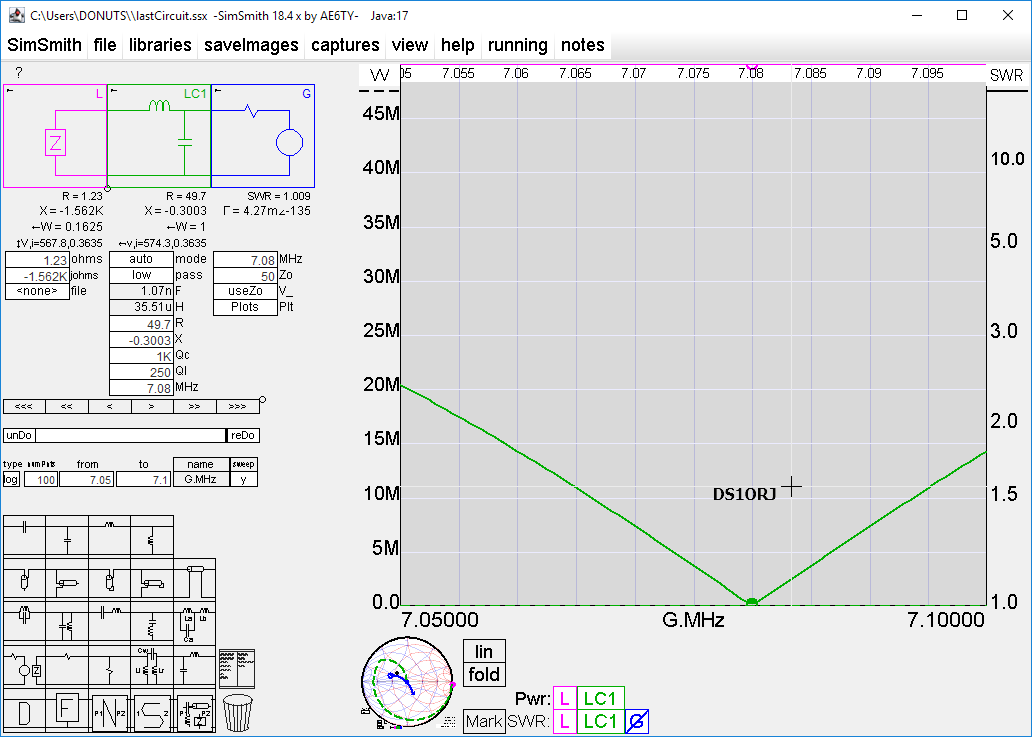
SimSmith 다운로드 및 기본 사용법은 아래를 참고한다.
https://ds1orj.tistory.com/184
임피던스 매칭 (2) 스미스차트 SimSmith
이 글에서는 아마추어 관점에서 간단한 프로그램을 통해 스미스차트의 기본에 대해 알아본다. 스미스 차트는 복잡한 임피던스를 시각화 하는 도구라고 생각할 수 있다. 다른 말로 하면 임피던
ds1orj.tistory.com
Q 250 : 7.066~7.093
Q 500 : 7.072~7.088
Q 1000: 7.075~7.085
Q 2000: 7.076~7.084
Q 4000: 7.077~7.083
Q 가 오르면 대역폭이 심각하게 줄어들므로 무조건 Q 가 높은 것이 유리한 것은 아니라는 것을 알 수 있다.
(일부 안테나의 경우 대역폭을 늘리기 위해 의도적으로 손실을 증가시켜 Q 를 내리는 경우가 있다)
여기까지 정리.
1. 대부분의 손실 및 임피던스 미스매칭은 로딩 코일의 저항(Q)으로 인해 발생한다.
실제 상황에서는 접지면(레디얼) 손실도 포함되며 경우에 따라 대부분의 손실이 레디얼(특히 차량)에서 발생 할 수 있다.
로딩은 모두가 아는대로, 사용할 수 있는 가장 두꺼운(리츠선이 최상) 와어어를 사용하는 것이 최상이다.
2. 로딩의 Q 가 너무 높으면(저손실 코일) 대역폭이 좁아지므로 사용이 어려울 것이다.
3. 수직 엘레먼트의 손실(두께)이 매우 큰 차이를 만들어 낼거라 생각하지만 수직 엘레먼트 두께(저항 손실) 자체는 전체 이득에 큰 차이를 만들지 않는다. (매칭 회로 없이 이득을 시뮬레이션 해보면 별 차이 없다)
4. 그러나 수직 엘레먼트가 두꺼워지면 로딩 코일의 필요 값이 줄어들므로 Q 역시 낮출 수 있다.
결과적으로 매칭 손실을 줄이고 대역폭을 늘릴 수 있다.
※ 이 시뮬레이션 결과는 베이스 로딩에 한정된다.
CM Base loading vertical antenna DS1ORJ
CE
SY length=2
SY wire=0.001/2
SY FREQ=7.08
GW 1 21 0 0 0 0 0 length wire
GE 1
EK
GN 1 0 0 0 0 0
LD 5 0 0 0 3.7665E7
EX 0 1 2 0 1 0 0 0
FR 0 0 0 0 FREQ 0
EN

